(Lesson Courtesy youcandothecube.com) Level: Grades 9-12. Time Required: One 50-minute class and homework time. Lesson pdf

Rubik’s Cube Geometry Lesson

Rubik’s cube is an enduring favorite of both kids and adults  who love a challenge. Today, educators are  exploring various ways to use it to teach math concepts such as area, perimeter, volume, angles, algorithms and enumeration, as well as  general skills in focus, sequencing, memorization, and problem solving. This lesson introduces students to the cube to help them better understand solid geometry.

National Standards

Instructional programs from pre-kindergarten through grade 12 should enable all students to:

• Analyze properties and determine attributes of two- and three-dimensional objects
• Visualize three-dimensional objects and spaces from different perspectives and analyze their cross sections
• Use geometric models to gain insights into, and answer questions in, other areas of mathematics
• Apply transformations and use symmetry to analyze mathematical situations

21st Century Skills

Learning and Innovation Skills

• Critical Thinking and Problem Solving
  • Exercising sound reasoning in understanding

Life and Career Skills

• Initiative & Self-Direction
  • Monitoring one’s own understanding and learning needs

Objective

1) To introduce the Rubik’s Cube and help students become familiar with its structure and associated terminology in order to understand the solution guide and better understand solid geometry.

Students will:

• Know the terminology associated with cubes and other geometric solids

• Understand the relationships between the center, edge, and corner pieces of the Rubik’s Cube

2) To learn the language of the solution guide and how to solve the white cross in order to complete the first step in solving the cube.

Students will:

• Be able to solve the white cross

• Know two methods/algorithms

Materials

• Class set of Rubik’s Cubes

• Solution_Guide pdf for the teacher. Also see the online version and Spanish version (pdf)

• Page 1 and 2 (Stage 1: Get to know your Rubik’s Cube) of Solution Guide for each student

• Page 3 (Stage 2: Solve the White Cross) of Solution Guide for each student

• Homework Activity pdf

• Pencils and Paper

Procedure

1. Introduce the Rubik’s cube through a brief history: (5 min.)

Erno Rubik’s (an interior design instructor born in Budapest, Hungary) initial attraction to inventing the Cube was not in producing the best selling toy puzzle in history. The structural design problem interested Rubik; he asked, “How could the blocks move independently without falling apart?” In Rubik’s Cube, twenty-six individual little cubes or “cubies” make up the big Cube. Each layer of nine cubies can twist and the layers can overlap. Any three squares in a row, except diagonally, can join a new layer. Rubik’s initial attempt to use elastic bands failed, his solution was to have the blocks hold themselves together by their shape. Rubik hand carved and assembled the little cubies together. He marked each side of the big Cube with adhesive paper of a different color, and started twisting. The Cube, as a puzzle, was invented in the spring of 1974, when the twenty-nine year old Rubik discovered it was not so easy to realign the colors to match on all six sides. He was not sure he would ever be able to return his invention to its original position. He theorized that by randomly twisting the Cube he would never be able to fix it in a lifetime, which later turns out to be more than correct. He began working out a solution, starting with aligning the eight corner cubies. He discovered certain sequences of moves for rearranging just a few cubies at a time. Within a month, he had the puzzle solved and an amazing journey lay ahead.

2. Distribute cubes and Page 1 and 2 (stage 1) of the solution guide. Ask students to disassemble, sort pieces, reassemble their cube, and use the solution guide to get to know the cube. Read through both pages with students. Be sure to explain the counter-clockwise/inverted language. (15 min.)

3. Discuss with students: (5 min.)

• A geometric solid is a 3-dimensional object with faces, vertices, and edges.

• A cube is a prism with 6 faces, all congruent squares.

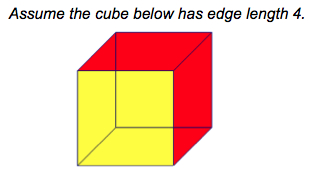
• The Rubik’s Cube is known as a 3×3. If it were made up entirely of smaller cubes, it would have volume 27 and surface area 54.

• The Rubik’s Cube has 8 corner pieces, 12 edge pieces and 6 (fixed) center pieces.

Ask the students: since 8 + 12 + 6 = 26, what happened to the 27th piece?

4. Distribute Page 3 (Stage 2) of the solution guide. Read through it with the students and demonstrate the method and algorithm. (15 min.)

5. Pass out the Homework Activity sheet and review. (5 min.)

——————————————————————–

Homework Activity

Vocabulary:

• faces
• bases (top and bottom)
• edges
• lateral faces
• vertices
• lateral edges
• prism
• cube

Exercises
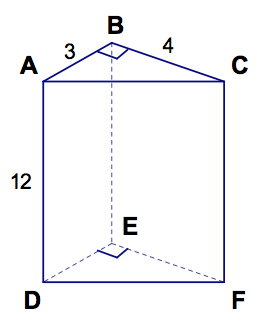1.    Name the bases of the prism: ∆ABC and_______

2.    Name the lateral faces of the prism. _______ _______ _______

3.    What shape are the lateral faces of the prism?

4.    Name the lateral edges of the prism. _____ _____ _____

5.    What is the height of the prism?

6.    What is the perimeter of the base?

7.    What is the total area of all of the faces?

8.    How many vertices does the figure have?

9.    How many edges does the figure have?

10. How many faces does the figure have?

11. How many faces does a cube have?

12. What is the shape of each face on a cube?

13. What is the area of one of the faces of the cube you drew above?

14. How many edges does a cube have?

15. How many vertices does a cube have?

16. If the cube above were a Rubik’s Cube, it would have how many:

a. Center pieces? b. Corner pieces? c. Edge pieces?

The BASE AREA of a prism is defined as the combined area of both bases. Commonly, it is referred to as Top & Bottom. For the Rubik’s Cube, we call them Up and Down faces.

17. What is the base area of the cube above? The LATERAL AREA of a prism is defined as the combined area of all the lateral faces. Commonly, it is referred to as Front, Back, Right and Left. It is the same for the Rubik’s Cube.

18. What is the base area of the cube above?

19. What is the total surface area of the cube above?

20. If the cube above was made up of smaller unit cubes, how many would it have?

Review the Cube:

21. How many edge pieces does it have?

22. How many corner pieces does it have?

23. How many center pieces does it have?

24. Add all the numbers of pieces from parts a, b, c. Write the sum here:

25. What is the volume of a 3x3x3 cube?

Can you remember the sequence we learned today that flips the edge piece around? Explain:

————————————————————————————–

Notes to Teacher

Here is a video clip that does a good job of instructing how to take the cube apart and reassemble it:

[youtube]http://www.youtube.com/watch?v=jdS_uvdl_JU[/youtube]

The White Cross: If students have trouble solving the white cross after reading the solution guide, explain that the general strategy is to put the white edge pieces down in the bottom layer, turn the bottom layer until the piece lines up with its correct center mate, and then spin that layer 180 degrees to put the white edge piece on the top. If it is flipped, use the algorithm in the guide to flip it back. This is an excellent lesson to get the students to better understand rotations. All the corner and edge pieces rotate around the center pieces (center of rotation). At this point the students should be instructed to come up and get the same numbered cube as the previous day.

Here is a video clip that does a good job of instructing how to solve the white cross: [youtube]http://www.youtube.com/watch?v=HsQIoPyfQzM[/youtube]

Additional Lessons and Exercises

Visit the youcandothecube.com Website for more lessons, most of which include a teacher’s instruction page, homework sheet, and answer key. Teachers and educational consultants have written, tested, and aligned these math lessons with national standards, states’ frameworks and 21st Century Skills.

© 2008 Seven Towns Limited Rubik’s ® is a registered trademark of Seven Towns, Ltd. London, England www.youcandothecube.com

Filed under: Grades 9-12, Lesson Plans

Tags: Geometry, Grades 9-12, Mathematics