(Lesson Courtesy the Exploratorium Museum, Maurice Bazin and Modesto Tamez. ) Level: Grades 6-12. Time Required: 1 to 2 hours; 2 to 3 class periods. Lesson pdf

Mayan Calendar Round — Keeping Time

Overview

In this lesson, which combines mathematics, engineering, and history, students in grades 6-12 learn about the ancient calendar system of the Maya, a Native American people of south Mexico and Northern Central America. In constructing a simple model of a calendar round, they solve the problem of how often the two time cycles coincided and learn about:

• The Mayan calendar system and calendar rounds
• The smallest common multiple of two numbers
• Prime numbers and how they are used to find smallest common multiples

Pre-requisite knowledge

Students should be familiar with the concept of prime numbers and know how to use a compass and protractor to make circles of different diameters.

The Mayan temple of El Castillo in Chichén Itzá is a huge stone pyramid that rises out of the Mexican jungle on the Yucatán Peninsula. It is probably no accident that there are 90 steps on each of the pyramid’s four sides, a total of 360 stepsc— the same as the number of regular days in the Mayan calendar year.

Background

As you celebrate New Year’s Day each year, do you consider how often it comes around — and why, with the calendar most of us use, a new year begins every 365 days? Suppose you had two calendars to follow, each with a different number of days? A new year would begin at a different point on each calendar. How often would the two New Year’s Days occur on the same day? Figuring that out is a mathematical problem the Maya solved through specially designed “calendars,” or “rounds.”

The Maya, who came to prominence in the New World in the third century a.d., kept extensive records of possessions, important dates, and astronomical observations. They were sophisticated in their understanding of science and math and had an advanced knowledge of astronomy, developed through observation and calculation.

For the Maya, religion, math, astronomy, architecture, and culture were all interrelated. People still gather at the Mayan city of Chichén Itzá at the equinoxes (the two days each year when day and night are of equal length) to watch a sunrise, when the shadow of the serpent carved along the grand stairway of the Temple of El Castillo (above) seems to snake its way up the pyramid’s side.

The Maya blended together their complex mathematics and precise astronomy in a cycle known as the “Calendar Round.” They used two different calendars — one for the haab, an astronomical year of 365 days, and one for the tzolkin, a ritual year of 260 days.

The haab was related to seasonal changes and agriculture, and corresponds to most calendars in use today, with a few differences. It had 18 months of 20 days each. The five days that were left over, known as uayeb, were considered unlucky.

The 260-day cycle of the ritual calendar, the tzolkin, can be inferred from the Dresden Codex, one of the few Mayan books that still exist today.

In that manuscript, dates are written as a combination of vertical bars and dots (representing the numbers 1 to 13), followed by one of 20 roundish glyphs, which are the names of individual days. Each date is written with one number and one glyph. So the total possible number of days for one cycle of the ritual calendar is 13 x 20, or 260 days.

The Maya believed in the continuing cycles of their world, so the moments when the haab and the tzolkin came together were important events.

Image, right: A detail of the Dresden Codex, one of the few surviving Mayan books. The bars and dots represent numbers ; the roundish glyphs are the names of individual days.

The Mayan Calendar Round

The 52-year cycle in Mayan life has been called a “calendar round” because it involves the ways of counting days in both calendars, and leads to to a new start for both calendars at the same time. Scholars have found a large number of numerical tables of multiples of 52 in the Dresden Codex

Anthropologists have known for a long time that a cycle of 52 astronomical years was important in the social life of the Maya. Every 52 years the Maya extinguished all fires in their households and threw away all their clay utensils. Then they “renewed” their social life by bringing a new fire ( el fuego nuevo) from a central location into all the villages and cities. The last time the Maya celebrated el fuego nuevo, the beginning of the 52-year cycle, was shortly before the Spanish conquest. By our calendar, that was in December of 1507. For the Maya, this last celebration of the calendar round occurred in the month of Yaxkin.

Counting for a Long, Long Time

The Maya had an even longer view of their calendar than the cycle of the haab and tzolkin together. There is a calendar called the “Long Count” that was used to record dates over long periods of time. The long count “year,” called a tun, has 360 days. A period of 20 tuns (7,200 days) is called a katun, and 20 katuns (144,000 days) is called a baktun. A period of 13 baktuns is called the “Great Cycle” of the Long Count. It is 5,200 years long (in 360-day years). The current Great Cycle will come ot an end on what most ofus will called December 21, 2012 (the winter solstice), which will be a significant date to modern Maya people.

Materials

For each group:

• 3 sheet of posterboard or thin cardboard, 11 x 14 or larger (to use for the gears)
• A sheet of heavy cardboard 9 x 12 inches or larger (to use as the base)
• Compass
• Thumbtacks or pushpins
• Protractor
• Scissors
• Lesson pdf (optional)

Activity Procedure: Making Gears

Provide students with the background on Mayan calendars and time-keeping. Explain that the class will undertake to make a basic model of the meshing Mayan calendars, in this activity that relies upon careful mathematical calculations. This activity can be done in small groups of 2-3 students.

Instructions for Students

In order to figure out how the two Mayan calendars meshed, you will need to construct simple gears, as described below.

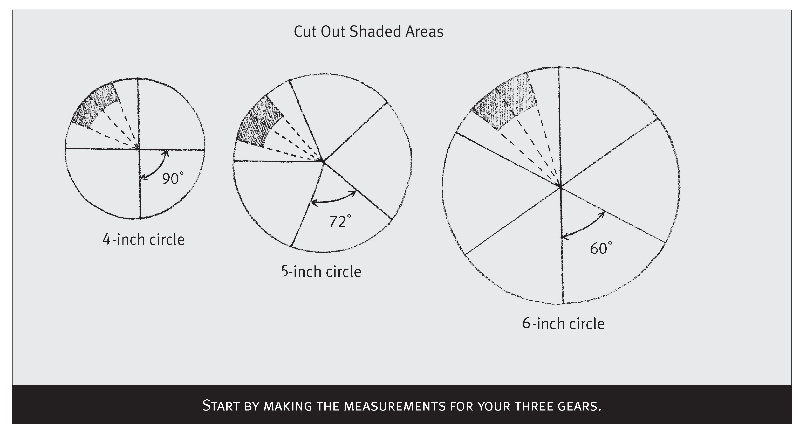
1. Use a compass to draw three circles out of poster board. One circle should have a 4-inch diameter, one a 5-inch diameter, and one a 6-inch diameter.

2. Use your protractor to draw lines that:

• Divide the 4-inch circle into four equal parts (90° each).
• Divide the 5-inch circle into five equal parts (72° each).
• Divide the 6-inch circle into six equal parts (60° each). See illustration above.

3. Each gear needs to have a number of teeth equal to its diameter in inches. That means, for example, that the 4-inch circle will have four teeth. How can you make four teeth and four spaces of equal width?

• Divide each quadrant of your 4- inch circle into four equal wedges, like slices of pizza. See illustration above.

4. Carefully cut out the circles. Then use the lines of the two inner wedges in each quadrant as guides to cut out the teeth. Cut about one-third of the way to the center of the circle.

When you’re done, you’ll have a gear with four teeth and four spaces of equal width. Use the same method to make five equal teeth and spaces on the 5-inch circle, and six equal teeth and spaces on the 6-inch circle. Again, the drawings above will help guide you.

5. Put two of the gears together and see how well they turn against each other. You’ll notice that the teeth of one gear probably won’t fit perfectly into the spaces of the other. Trim the sharp outer corners of the teeth on all three gears to make sure they mesh together well. (If you look at the gears of a mechanical device such as a clock, you’ll notice that the edges of the teeth on those gears are also rounded off to make the teeth and spaces mesh properly.) Trim your gear teeth a little at a time, until they mesh smoothly.

6. When you’re done constructing your gears, you need to label them.

• First, label the teeth of the 4-inch gear 1, 2, 3, 4, going counter-clockwise, as shown on the next page. This will represent a four-day year.
• Next, label the spaces of the 5- inch gear with the numbers 1, 2, 3, 4, 5, going clockwise, to represent a five-day year.
• Finally, label the spaces of the 6-inch gear 1, 2, 3, 4, 5, 6, going clockwise, to represent a six-day year.

Procedure: Meshing Gears

Each gear you made represents one way of grouping days. In this sense, each one is a calendar.

1. To begin your investigation, set the 6-inch gear aside. You’ll need it later.

2. Now put a thumbtack or push- pin through the center of the 5-inch gear, and pin it to a large piece of cardboard to hold it in place. Set tooth 1 of the 4-inch gear in space 1 of the 5-inch gear. Then pin the 4- inch gear into place. Turn the gears a little to make sure they’re meshing well.

3. Now, let time flow and the days mesh as you turn both gears. How many turns of each wheel does it take before you’re back to the starting position—with the same tooth 1 and space 1 meshing together again?

4. If you let the smaller gear make one revolution clockwise, tooth 1 will be in space 5 of the larger gear. After the next revolution of the smaller gear, tooth 1 will be in space 4. Keep turning the smaller gear until tooth 1 falls again into space 1 of the larger gear. How many revolutions did each gear have to make? You’ll find that the 4-inch gear made five revolutions and the 5-inch gear made four revolutions.

To visualize these cycles, imagine putting ink on the edges of the gears and rolling them along a piece of paper in a straight line. One turn of the 4-inch gear gives you a group of four marks. One turn of the 5-inch gear gives you a group of five marks.

How many marks will you have to make before “groups of 4” and “groups of 5” coincide?

You’ll find that five turns of the 4-inch gear (five groups of 4) will bring you to the same place as four turns of the 5-inch gear (four groups of 5). At the twentieth mark, both will coincide again.

4 x 5 = 20

5 x 4 = 20

Working with Larger Numbers

If the 4-inch gear and 5-inch gear represent two different calendars of 4 days and 5 days, we can say that there is a 20-day cycle in the system using both calendars. Every 20 days, they will come together again. Once every 20 days, it will be New Year’s Day on both cardboard-gear calendars.

Counting and Calendars

But what about the two Mayan calendars, with 365 days and 260 days? Will it take 94,900 days (365 x 260) for the two New Year’s Days to happen together again? That’s only once every 260 astronomical years!

You can use the 6-inch gear and the 4-inch gear to see that the two New Year’s Days will actually coincide in a much shorter time.

1. Take the 5-inch gear off the cardboard base and set it aside. Pin the 6-inch gear onto the base so that tooth 1 of the 4-inch gear meshes with space 1 of the 6-inch gear. Make sure these two gears mesh smoothly.

2. Now turn the gears. How many times does each gear revolve before tooth 1 and space 1 line up again? You’ll find that tooth 1 and space 1 mesh again after only two turns of the 6-inch gear and three turns of the 4-inch gear.

Why is this so? Imagine again that you ink and roll each gear on its edge. One turn of the 4-inch gear gives you a group of four marks. One turn of the 6-inch gear gives you a group of six marks. When do the two groupings end together?

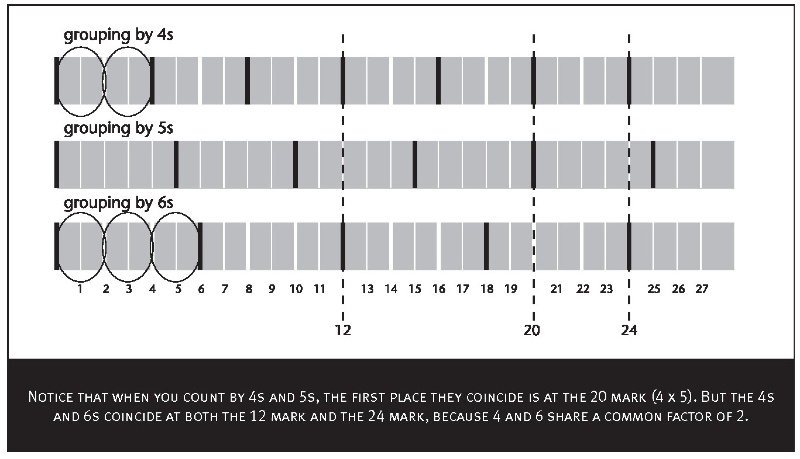
The 4-inch and 6-inch gears coincide at the twelfth mark. This corresponds to the mathematical idea of the smallest common multiple — that is, 12 is the first number that contains both “groups of 4” and “groups of 6.”

3 x 4 = 12

2 x 6 = 12

Why did the 4- and 5-inch gears have to complete the full 20 (4 x 5) turns while the 4- and 6-inch gears didn’t have to turn the full 24 times (4×6)?

3. Look at the first and third lines in the illustration below, showing the results of “grouping by 4s” and “grouping by 6s.” Notice that each group contains a smaller internal grouping—“groups of 2.” That means that 4 and 6 share a common factor of 2.

6 = 3 x 2 (three groups of 2)

4 = 2 x 2 (two groups of 2)

If you multiply 6 x 4, then factor out the common 2 (divide by 2), you get the smallest common multiple of 6 and 4, which is 12.
There is no smaller common internal grouping—no common fac- tor—for the numbers 4 and 5, so those gears had to complete the full 20 turns.

Putting the Mayan Calendars Together: Prime Numbers

Notice that when you count by 4s and 5s, the first place they coincide is at the 20 mark (4 x 5). But the 4s and 6s coincide at both the 12 mark and the 24 mark, because 4 and 6 share a common factor of 2.

Now imagine that you have a gear for each Mayan calendar. One gear has 260 teeth and the other has 365 teeth. When we mesh tooth 1 of one calendar with space 1 of the other, it’s the first day of the year for both calendars. Then time moves on and the gears turn. How long will it take before the two years begin on the same day again?

To find out how long it will take for the two Mayan calendars to coincide, you’ll need to find the smallest common multiple for the numbers 365 and 260. To do that, you need to start by finding all the numbers by which 365 and 260 can be divided exactly.

This process is called finding the prime factors of a number. Prime factors are all the factors of a number that are prime numbers.

Prime numbers are numbers that can be divided exactly only by themselves and 1. For example, 7 is a prime number because it can be divided only by 1 and itself. But 9 is not a prime number because it can also be divided by 3.

The first ten prime numbers are 1, 2, 3, 5, 7, 11, 13, 17, 19, and 23.

1. To find the prime factors of 260, the number of days in the Mayan ritual calendar, begin by dividing 260 by 2. Keep dividing by 2 until the result is an odd number. (You can’t divide an odd number exactly by 2.) Then try dividing that odd number by the next prime number—3. Divide by 3 as many times as you can. Then try dividing by 5, and so on.

2. Try finding the prime factors of 260.

The prime factors of 260 are 2 x 2 x 5 x 13.

3. Now, do the same thing with the prime factors of 365, the number of days in the Mayan astronomical calendar.
You probably discovered quickly that you can’t divide 365 exactly by 2 or by 3. But you can divide it by 5, which gives you a result of 73. When you try to divide 73 by successive prime numbers, you will discover that 73 is itself a prime number!

The number 365 can only be factored into 5 x 73. The numbers 260 and 365 share only one common factor: 5.

260 = 5 x 52

365 = 5 x 73

4. Now that you know this, can you figure out the smallest common multiple for 260 and 365?
If you factor out the common 5 (that is, divide by 5), you get 18,980 (5 x 73 x 52), which is the smallest common multiple of 260 and 365. What does that tell you about when the two Mayan calendars coincide?

As you have discovered, exactly 18,980 days will pass before the two New Year’s Days occur on the same day again. They will come together again after 52 astronomical years of 365 days each, which is the same amount of time as 73 ritual years of 260 days each.

Extensions

• Have students ask their grandparents or the oldest people they know in their family or community, about times
  of renewal, such as New Year’s Day, Chinese New Year, and Rosh Hashanah. Do they know of other older traditions, or traditions from other cultures, used to mark renewal?

• Ask students we estimate the age of someone born on February 29, a date that occurs only every four years, during a “Leap Year.” How often would a person celebrate his or her real birthday? How “old” would they be now if they counted only that day as their birth date?

• Have students research different cultures of Central and South America, past and present, including the Inca, who were remarkable engineers. Be sure to read our eGFI article the engineering feat of Machu Picchu.

Resources

• Related Exploratorium Webpages: Explore further about Chichén Itzá; learn more about the Maya counting system, find more resources on the Maya; and learn about another ancient observatory, the Chaco Canyon.

• “Ancient Observatories, Timeless Knowledge,” a NASA-sponsored Website

• “Native American Connections,” part of NASA’s “Ancient Observatories,” focuses on images and activities that have been used by Native Americans for generations to explore Sun-Earth science.

The Mayan Calendar and Calendars Through the Ages, two helpful web pages maintained by Webexhibits.org

A Walk Through Time: The Evolution of Time Measurement through the Ages. A Web page maintained by The National Institute of Standards and Technology (NIST).

Coe, Michael D. The Maya. New York: Thames and Hudson, 1999.

Malmstrom, Vincent H. Cycles of the Sun, Mysteries of the Moon: The Calendar in Mesoamerican Civilization. Austin: University of Texas Press, 1997.

Sharer, Robert J. Daily Life in Maya Civilization. Westport, CT: Greenwood Publishing Group, 1996.

This activity was developed by by Maurice Bazin and Modesto Tamez. Image credits: Black-and-white images culled from the lesson pdfs. All other images from Wikimedia Commons.

Filed under: Grades 6-8, Grades 9-12, Lesson Plans

Tags: Astronomy, Engineering in History, Grades 6-12, History, Mathematics