Lesson: Build a Catapult
 (Lesson Courtesy the Cornell Center for Materials Research (CCMR). Level: Grades 5-12. Group size: 2-4 students. Time Required: Two or three 60-minute class periods. Lesson PDF.
(Lesson Courtesy the Cornell Center for Materials Research (CCMR). Level: Grades 5-12. Group size: 2-4 students. Time Required: Two or three 60-minute class periods. Lesson PDF.
**Please note: Teachers who do not borrow the catapult kits from CCMR will need to gather and construct the materials for this activity — dimensions for the wooden materials are provided below.
Overview
In this lesson, students in grades 4-12 learn about the history of catapults and how they work. They assemble their own catapult model, making adjustments to improve its performance. Students gain engineering experience while learning principles of physics and working with the scientific processes of experimentation and trial and error.
SAFETY:
- Warn the class that the only item to be used in the catapult as a projectile is the whiffle ball. Use of any other material will result in the immediate dismissal of the team.
- Make sure no students are in the catapult’s trajectory before triggering it.
Objectives
Students will gain an experience in engineering while learning principles of physics and working with the scientific processes of experimentation and trial and error.
Students will:
- Be introduced to the history of catapults and the theory of how they work
- Learn physics vocabulary terms
- Assemble a basic catapult
- Observe the changes in the catapult’s performance after adjustments
- Record their catapult’s performance
- Compete to test their team catapult’s accuracy at hitting targets at various distances
Standards
Next Generation Science Standards
- Define the criteria and constraints of a design problem with sufficient precision to ensure a successful solution, taking into account relevant scientific principles and potential impacts on people and the natural environment that may limit possible solutions. [Grades 6 – 8]
Common Core State Mathematics Standards
- Summarize numerical data sets in relation to their context, such as reporting the number of observations, or describing the nature of the attribute under investigation, including how it was measured and its units of measurement. (Grade 6)
- Recognize that a measure of center for a numerical data set summarizes all of its values with a single number, while a measure of variation describes how its values vary with a single number. (Grade 6)
International Technology and Engineering Educators Association
- Specify criteria and constraints for the design. [Grades 6 – 8]
- Make two-dimensional and three-dimensional representations of the designed solution. [Grades 6 – 8]
New York State – Elementary Science 1997
Standard 1 – Analysis, Inquiry and Design
Standard 4.5 – The Energy and matter interact through
forces that result in changes in motion
Standard 7 – Interdisciplinary Problem Solving
Vocabulary
Potential Energy, Kinetic Energy,
Trajectory — The path or curve described by a body (as a planet or projectile) under the action of given forces.
Potential Energy — The kind of energy that a body has by virtue of its position. When a body is raised to a higher level, it is able to do a certain amount of work in falling back again, and hence it was given a certain amount of potential energy in raising it.
Kinetic Energy — The energy that a body has by virtue of its motion.
Energy Storage — If a spring is compressed, and then is forced to stay in that compressed configuration, the spring can be said to have “stored” energy. Once the spring is released, it will return to its original configuration (usually expending the stored energy as rapidly as possible). The same goes for stretching a spring; when released, it will collapse back to its original configuration.
Trigger — The device used to release the catapult once it has been loaded and charged to fire the projectile.
Ballistics — The science of projectiles.
Range — Distance for which a projectile can be thrown.
Materials
For the teacher:
For Class:
Phillips Screwdrivers
For each student:
For each pair of students:
Catapult Kit:
- 4 Rubber bands
- Pushpin
- 2 Nuts (1/4 x 20)
- 2 Machine Screws, for arm placement (1/4 x 20 x 4 1/2 in.) – ¼ x 20 x 4¼” (nuts – ¼ x 20)
- 4 Drywall Screws
- 4 Screw Eyes (Open Eye)
- Screw driver
- Hook & Chain (Chain, approx. 11.5 in.)
- Sturdy string or rope
- Wooden Base (measurements: Base – L 16 in. / W 3.5 in. / H .75 in., with holes drilled approx. 1 in. from either end for the hooks, and holes drilled on the side to attach pegboard)
- Wooden Arm (measurements: L 16 in. / W 1.5 in. / H .75 in. (with holes drilled at 5 in., 6 in., 7 in., 8 in. , 9 in. to vary arm length)
- 2 Pegboard Sides (measurements: Base 12 in. / Top 2 in. / Height 13 in., with 1 in.between pegboard holes)
- Tape
- Whiffle ball or other light material, such as cotton balls
Note: these kits can be constructed and assembled by the teacher or borrowed from CCMR. To borrow a kit, please apply online. Please note that there is limited availability of kits, which must be requested 2 weeks prior to shipment date. For more information, please contact the lending librarian, Kevin Dilley at 607-254-8256.
Background
Over 2000 years ago, the Greeks and Romans did not know about gunpowder, yet were able to hurl projectiles over a large distance using kinetic energy storage devices. Through the years, some modifications were made to increase the accuracy and throwing distance of these machines. The first two types of throwing machines were the catapult and the ballista. The catapult started out as a large cross bow to shoot oversized arrows at an enemy. The ballista was about 10 times larger than a catapult and threw large stones.
The ballista’s design consists of two pieces of wood, each fastened at one end to a torsion device rotating about a more or less horizontal axis. The free ends of the wooden pieces are connected together with a rope. The projectile to be thrown is held by the connecting rope used as a sling.
When most people think of the catapult, they are actually thinking about an onager. The strange name is derived from a wild donkey kicking with its hind legs. The onager (or gone, mangonel, or nag) was typically a single spar held in a more or less vertical position by a torsion device rotating around a horizontal axis. The projectile was located in either a pocket at the top end of the spar or in an attached sling.
The choice of the Middle Ages was a trebuchet. This device used gravity instead of torsion springs to provide propulsion energy. The theory is simple: put a large weight at the short end of a lever arm and put the projectile in some kind of basket at the other end of the lever. The velocity of the projectile can become quite large when the ratio of the lengths of the lever arms is great. Incidentally, the trebuchet was also used as a punishment device called the ducking stool. People were placed in a seat at the long end and successively ducked into a pool of water.
The catapult is still in use today, although radically different from those used in history. The modern catapult is used to launch aircraft from the deck of an aircraft carrier. The aircraft carrier catapult uses steam as a source of energy to push a piston along a linear track in the aircraft carrier’s deck. The piston pushes the aircraft and accelerates the plane up to flying speed in a very short distance. The same kind of mechanism can be found at Knott’s Berry Farm, where it propels the Montezuma’s Revenge roller coaster ride.
Pre-Activity Preparation
1. Photocopy print materials (Activity Sheets 1-5) for each student. *Please note, eGFI has supplied additional instructions, above, to clarify the construction of the catapult.
2. Have students conduct research on the subjects of catapult, trebuchet, and onager before beginning this assignment.
3. Construct a target range (see Supplemental Information below).
Classroom Procedure:
SAFETY:
- Warn class that the only item to be used in the catapult as a projectile is the whiffle ball. Use of any other material will result in the immediate dismissal of the team.
- Make sure no students are in the catapult’s trajectory before triggering it.
Engage (Time: 20 mins)
Discuss the history and types of catapults outlined in “Science Content” with the students. Discuss physics terminology. Have the students engage in a discussion on how to adjust the catapult to vary the distance to which it can throw a projectile (refer to Activity Sheet 1: Catapult Variables for the list of adjustments which will provide variables to catapult performance). Discuss the adjustments and how they would affect performance.
Explore (Time: Varies)
Inform students that there will be a competition to test their catapult’s accuracy at hitting targets at various distances. Divide students into groups of two to four, and allow them to begin construction of their catapults. Assist as necessary and use step-by-step guide (refer to Assembly Instructions and Activity Sheet 2). *Please note that eGFI has supplied additional instructions, above, to clarify the construction steps. Encourage students to discuss the physics principles and vocabulary they learned as they construct their catapult to increase their understanding.
Assembly Instructions
SAFETY:
- Warn class that the only item to be used in the catapult as a projectile is the whiffle ball. Use of any other material will result in the immediate dismissal of the team.
- Make sure no students are in the catapult’s trajectory before triggering it.
1. Distribute the catapult kits, and have students lay out and check their materials.
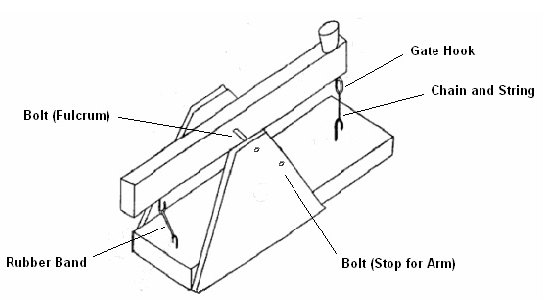
2. Have teams align their sides by inserting the machine screw through one of the top holes of one side, followed by a spacer, the lever arm, another spacer, and then the corresponding hole on the second side. Secure this with a nut, making sure to leave it just loose enough for the arm to swing freely.
3. Have students align the sides with the base and screw in the dry wall screws to secure it. These are represented by the x’s in the picture below.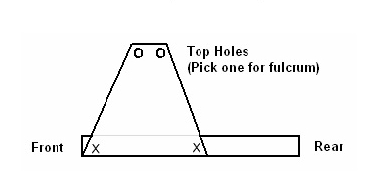
4. Now install the second bolt as a stop for the arm. Make sure it is below and closer to the rear compared to the fulcrum. You need not make it terribly tight.
5. Now install the hook eyes at both ends of the base and both ends of the lever arm as shown below.
6. Install the hardware in appropriate location(variable).
Caution: The length of chain with the gate-hook and attached string which acts as a trigger device should always be mounted on the catapult base, with the separate gate-hook eye ONLY being mounted on the catapult arm as shown above. At no time should the jack-chain with the gate-hook attached be flying through the air in an arc at the end of the catapult arm when the catapult is triggered.
7. Use 2 rubber bands at the front of the catapult, then firmly attach the string to the chain, and slip the string through the gate hook. Pull the string taut to create the tension. If it cannot be pulled taut, the chain needs to be shortened. Release the string to launch the catapult.
8. Install cup on the lever arm(used to hold the whiffle ball), attaching it with strong packaging tape.
9. Place the whiffle balls inside the cup.
10. Test and adjust catapults for the competition.
Set up the target range in the classroom for the competition. Distribute whiffle balls to each student. Tell them they will use these to test their catapults and let them practice hitting the targets.
If time permits, have the students experiment with variables (Activity Sheet 3) to refine and improve performance.
Next, discuss the scoring system for the competition. Explain how teams should take data on their own performance (See Assessment, below) and let the competition begin!
Explain (Time: 10 mins) Discuss with students what did and did not work, have them explain why certain settings worked better than others. Distribute Activity Sheet 5: Catapult Science Challenge Questions as a homework assignment to each student. Allow the students to work on it with their team members. During the next class period, discuss the challenge questions and clear up any misunderstandings the students may have about the concepts they learned.
Assessment
The following rubric can be used to assess students during each part of the activity. The term “expectations” here refers to the content, process and attitudinal goals for this activity. Evidence for understanding may be in the form of oral as well as written communication, both with the teacher as well as observed communication with other students. Specifics are listed in the table below.
1= exceeds expectations
2= meets expectations consistently
3= meets expectations occasionally
4= not meeting expectations
| Engage | Explore | Explain | |
| 1 | Shows leadership in the discussion and offers creative ideas reflecting a good understanding of the physics behind the catapult. | Completes work accurately while providing an explanation for what is observed. Works very well with partner. | Provides an in-depth explanation of findings, making good use of vocabulary terms. Fills out worksheet clearly. |
| 2 | Participates in the brainstorm and shows an understanding of the physics related to the catapult. | Completes work accurately and works cooperatively with partner. | Provides clear explanation of findings. Fills out worksheet clearly. |
| 3 | Contributes to the brainstorm, but shows little understanding of catapult physics. | Works cooperatively with partner, but makes some mistakes with the procedure. | Provides a limited explanation of findings. Fills out some of the worksheet. |
| 4 | Does not participate in brainstorm. Shows no understanding of catapult physics. | Has trouble working with partner. Does little to complete the procedure. | Is not clear in explanation of findings. Does not fill out worksheet. |
Extensions
- Challenge students to adjust their catapult in order to throw the whiffle ball the longest distance possible.
- Encourage students to think about what other projectiles they could use, how they would perform, and why they would perform this way.
- Challenge questions are listed on the following three pages.
Engineering and Mathematics Exercises
These exercises were originally designed to relate science content to Future Scientists and Engineers of America projects. Some of the questions relate specifically to the project; others go well beyond the project. Questions may vary in complexity but teachers are encouraged to use them to provide further discussion at the completion of the hands-on project.
1. Name the various forms of energy involved in the catapult.
Answer: The forms of energy are: potential energy stored in the rubber band or springs, kinetic energy of the arm, kinetic energy of the whiffle ball, friction energy in the catapult mechanism, air friction of the ball as it is moving through the air, increased motion energy of the air molecules as the ball strikes and accelerates them, potential energy of the gravitational field as the ball rises and falls back to earth, compression energy as the ball crashes into the earth, deforming both the ball and the earth, and heat energy as the earth is warmed up a little.
2. If one were to use a golf ball instead of a whiffle ball, would the ball go farther, everything else being equal?
Answer: Yes, the light whiffle ball with holes in it has a great deal of air resistance and slows down very quickly. The much heavier golf ball would have much more energy and go much farther. Even a ping-pong ball, which is about the same weight as a whiffle ball, would go farther due to the smooth surface instead of the holes.
3. If you were to do the project on the moon, which of the three balls would you expect to go the shortest distance?
Answer: The golf ball, because it is heavier. It would not reach as high a velocity as the other lighter balls and hence wouldn’t go as far. Since there is no air on the moon, there would be no air friction for either the whiffle or ping-pong balls.
4. Using the whiffle ball on earth, if you doubled the rubber bands, so the force would be twice as much, the whiffle ball would leave the cup at about twice the velocity. Would you expect it to go twice as far?
Answer: No, the friction would be much greater at the higher speed and the distance would be less than two times.
5. If the ball left the cup going parallel with the ground, would the time in the air be longer with two rubber bands as compared to one?
Answer: No: The horizontal velocity has nothing to do with the time the ball stays in the air. The force of gravity acts completely independent of the horizontal forces or velocities. The ball begins to fall when it leaves the cup and it falls exactly the same as if it were not moving.
6. If you didn’t have air friction, at what angle with the earth’s surface would give the greatest distance?
Answer: 45 degrees. This gives equal vertical and horizontal velocities, which is well known to give the largest distance. This can easily be proven mathematically, and has long been known by the military artillery folks.
7. If you tried to fire the catapult exactly the same every time, would you expect the ball to fall in the same place each time, or in some specific pattern that would have specific mathematical meaning?
Answer: Specific pattern. If you did a large number of shots in exactly the same way, you would find a specific pattern where the majority of the hits are close together and the others scattered about in a “Normal Distribution.” The way the distribution is spread depends on the various parameters of the catapult and how well they can be repeated each time.
8. If the ball leaves the catapult with a velocity V,what are the vertical and horizontal components?
Answer: Vertical velocity is V * sine(theta) and the horizontal velocity is V * cosine (theta), where theta is the angle between the velocity, V, and the horizontal.
9. If there is no air resistance, how high will the ball rise?
Answer: The ball will act like a falling body with an initial velocity V. The equation for a falling body is as follows:
H = Vv x T – (1/2) x g x T^2
Where H is the height in feet. T is the time in the air in seconds and g is the acceleration due to gravity (~ 32.2 ft/sec^2) and Vv is the vertical velocity equal to V x sine(theta).
Since both H and T are unknown, we need a second equation. This second equation is obtained from the falling body velocity equation:
Vt = Vv – g x T
Where Vt is the velocity at any time. Vt at the maximum height is zero, thus we have the equation Vv = gt. Substituting in the equation above we have:
H = ((Vv^2)/g) – (1/2) x g x (Vv/g)^2
H = (1/2) x (Vv^2)/g
Example: Assume the velocity is 90 ft/sec and the angle with the horizontal is 340 degrees, what is the height?
Vv = 90 x sin(340), Vv = 90 x .5 = 45 ft/sec
H = (1/2) x (45^2)/32.2 = 31 feet
10. How far would the ball go with no air friction in question 9?
Answer: 109 ft
T = 2 x (Vv/g) = 2 x (45/32.2) = 2.8 sec
Vh = V x cos(theta) = 90 x cos(30) = 90 x .866 = 78 ft/sec
Distance = Vh x T = 78 x 2.8 = 218 feet
11. Show that the maximum distance will be achieved with a 45-degree angle.
Answer: Combining the above equations, one obtains the range of the ball as a function of the angle with the horizon as follows:
H = (2/g) x (V^2) x sin(theta) x cos(theta)
Differentiating H with respect to theta and setting to zero.
d(h)/d(theta) = (2/g) x (V^2) x ((-sin(theta)^2) + (cos(theta)^2)
Setting this equal to zero makes sin(theta) = cos(theta) This is only true if theta is 45 degrees.
Supplemental Information
Target: A target may be constructed as follows: Bulls Eye — use a pie tin taped down. The diameter is approximately 1’ and when it hits it “pings,” which increases the thrill of the team able to acquire a direct hit. Middle and Outer rings—use 1⁄4” tubing, string, or rope lengths of 15.7’ and 9.4’ to form circles. Join ends of tubing with a 1⁄4 wood dowel as a plug. Tape tubes to the floor. Buckets as bullseyes can also make a nice target.
Scoring:
Event 1 – Inner 7; Middle 5; Outer 3
Event 2 – Inner 15; Middle 10; Outer 5
See Lesson PDF for scoring sheets.
Acknowledgments: Future Scientists and Engineers of America
Filed under: Class Activities, Grades 6-8, Grades 6-8, Grades 9-12, Grades K-5, Grades K-5, Lesson Plans
Tags: catapult, Class Activities, Engineering in History, forces and motion, Grades 5-12, Grades 6-8, Lesson Plan, Mathematics, Newton's Laws, Physical Science