Get Me Off This Planet!
This hands-on activity about the factors involved in getting astronauts off Mars is part of a TeachEngineering.org Mission to Mars curricular unit.
Grade level: 6 -8
Time: 45 minutes
Summary
In this lesson to teach middle school students how a spacecraft gets from the surface of the Earth to Mars, students first investigate rockets and how they are able to get us into space, then discuss the nature of an orbit as well as how orbits enable us to get from planet to planet.
Engineering Connection
After this lesson, students should be able to:
- Describe how a rocket must overcome the forces of gravity and drag in order to get out of the atmosphere.
- Explain that thrust is the force created by a rocket.
- Describe how an orbit is the balance of gravity and an object’s tendency to follow a straight path.
- Explain some challenges that engineers face in getting a rocket to Mars.
- Plan an investigation to provide evidence that the change in an object’s motion depends on the sum of the forces on the object and the mass of the object
- 2. Fluently divide multi-digit numbers using the standard algorithm. [Grade 6]
- 3. Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation. [Grade 6]
- 4. Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities. [Grade 7]
- 3. Use numbers expressed in the form of a single digit times an integer power of 10 to estimate very large or very small quantities, and to express how many times as much one is than the other. For example, estimate the population of the United States as 3 × 108 and the population of the world as 7 × 109, and determine that the world population is more than 20 times larger. [Grade 8]
- G. Transportation vehicles are made up of subsystems, such as structural propulsion, suspension, guidance, control, and support, that must function together for a system to work effectively. [Grades 6 – 8]
Next Generation Science Standards
- Plan an investigation to provide evidence that the change in an object’s motion depends on the sum of the forces on the object and the mass of the object. [Grades 6 – 8]
- Describe how a rocket must overcome the forces of gravity and drag in order to get out of the atmosphere.
- Explain that thrust is the force created by a rocket.
- Describe how an orbit is the balance of gravity and an object’s tendency to follow a straight path.
- Explain some challenges that engineers face in getting a rocket to Mars.
Getting off Earth – Launch
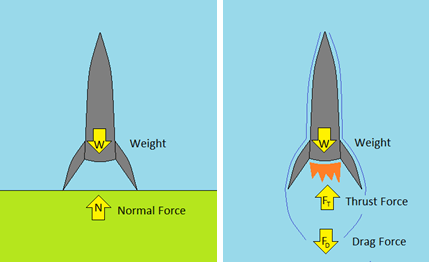
Let’s consider the forces acting on a rocket. Look at Figure 1 showing a rocket just before liftoff. The two forces acting upon the rocket in this scenario are the rocket’s weight (W) and a normal force (N). A normal force is a force that acts on an object by a contact surface (in this case, the ground). A normal force also acts perpendicularly to the surface – because the ground is horizontal, the normal force acts vertically. If we add the forces together, we will find the net force (Fnet) acting on the rocket: Fnet = N – W. The weight is preceded by a minus sign because the weight of the rocket acts downward (the normal force acts upward and is thus positive, but does not require a plus sign by common mathematical sign convention). It is easy to understand from this situation that because the rocket is not moving, the weight is balanced by the normal force: N = W. Thus, the net force is zero.
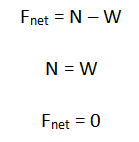
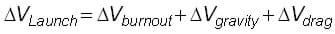
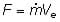
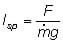
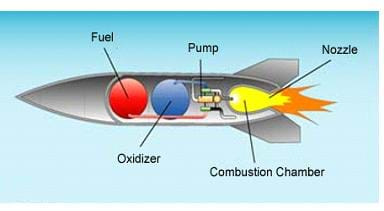

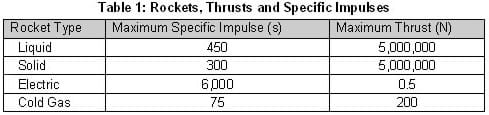
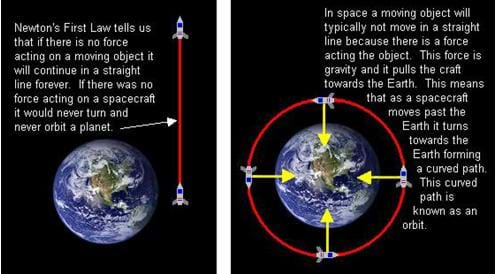
Orbits
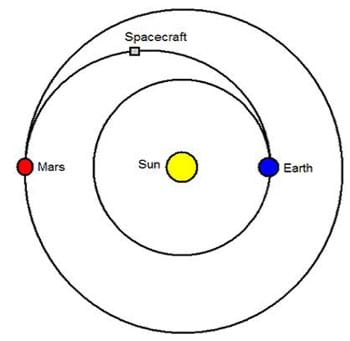
Getting to Mars
Vocabulary/Definitions
| apoapsis: | The point in an orbit farthest from the center of attraction (that is, the planet or sun). |
| chemical rocket: | A rocket that relies on a chemical combustion to create a super-heated, high-pressure gas that is used for thrust. |
| cold gas rocket: | A rocket that uses escaping pressurized gas as a source of thrust. |
| electrical rocket: | A rocket that creates thrust by using electricity to accelerate charged particles, which are directed out the back of the vehicle. |
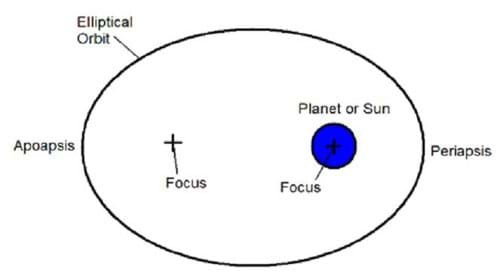
| ellipse: | A closed curve resembling a flattened circle. Most orbits are in the shape of an ellipse. |
| escape velocity: | The minimum velocity needed to escape from the gravitational pull of a celestial body (Earth, Sun, etc). |
| foci: | Two points on an ellipse in which the sum of the distances to the foci from any point on the ellipse is a constant. |
| Newton’s 1st Law of Motion: | For an object being acted on by balanced forces: if the object is at rest, it will remain at rest; if an object is in motion, it will remain in motion (“law of inertia”). |
| Newton’s 2nd Law of Motion: | For an object being acted on by unbalanced forces: the acceleration of an object is dependent on its mass and the net force. Described by the equation Fnet = ma. |
| Newton’s 3rd Law of Motion: | For every action, there is an equal and opposite reaction. |
| normal force: | A force provided by a contact surface (e.g., the ground) that acts perpendicularly to the surface. |
| orbit: | The path of a planet, moon, spacecraft, or any other object in space as it revolves around another object, such as the sun. |
| periapsis: | That point in an orbit closest to the center of attraction (that is, the planet or sun). |
| specific impulse: | A measure of rocket efficiency that is equal to the thrust of the rocket per weight of the fuel. |
| thrust: | The forward reaction to the rearward movement of exhaust from a rocket engine. |
| universal gravitational constant: | The constant that relates the gravity of two objects depending on their masses and the distance between them. |
Associated Activities
- The Great Gravity Escape – Students use water balloons and a length of string to understand how gravity and the speed of an orbiting body balance to form an orbit. They also see that when the velocity exceeds the escape velocity, the object will escape the gravity of the sun or planet that it is orbiting around.
Lesson Closure
Assessment
Pre-Lesson Assessment
- What does it take for us to get to Mars? What does it take to get a spacecraft off the ground?
- What do you know about rockets? How do they work? Can you name any rockets? (Answer: US space shuttles: Saturn, Atlas, Titan, Delta, Ariane, Pegasus, etc.)
- Once a spacecraft is out of the Earth’s atmosphere, it goes into an orbit. What is an orbit? (Answer: An orbit is a curved path on which a planet, star, spacecraft, etc. moves around another object or celestial body.)
- Is gravity acting on the space shuttle and its crew? (Answer: Gravity is acting on them and creates the centripetal force that keeps the space shuttle from flying in a straight line off into space. They do not feel it because the inertia of their orbit is perfectly balanced with the centripetal force from gravity.)
Post-Introduction Assessment
- Why does it take so much energy to get to Mars? (Possible answers: We have to overcome the gravity of Earth; we have to overcome the drag of Earth’s atmosphere; we have to get enough speed to get to Mars in a reasonable time; and/or we have to slow down once we get to Mars so we do not just fly past the planet.)
- If a rocket is moving at constant velocity and the thrust force is equal to the sum of its drag force and its weight, what will happen to the rocket? What law describes this situation? (Answers: The rocket will continue to move at the same velocity. Newton’s 1st Law of Motion.)
- If a rocket constant is moving at constant velocity and the thrust force is less than the sum of its drag force and its weight, what will happen to the rocket? What law describes this situation? (Answers: The rocket will begin to fall back to Earth. Newton’s 2nd Law of Motion.)
Lesson Summary Assessment
- Which of Newton’s laws of motion states that for every action there is an equal and opposite reaction? (Answer: Newton’s third law of motion.)
- What must a rocket overcome in order to reach orbit? (Answer: Gravity and drag.)
- What is the force created by a rocket called? (Answer: Thrust.)
- What do we call the measurement of a rocket’s efficiency? (Answer: Specific impulse.)
- What happens if a spacecraft in orbit slows down too much? (Answer: If the spacecraft slows down a little it moves into a lower orbit — closer to Earth; if the craft slows down too much it will not be able to maintain an orbit and will crash — if they did not mean to slow down — or land — if they did mean to slow down.)
- What happens if a spacecraft in orbit reaches the escape velocity? (Answer: The spacecraft will overcome the Earth’s gravity.)
- What do we call the point on an elliptical orbit that is furthest from the planet/Sun? (Answer: Apoapsis.)
- What do we call the point on an elliptical orbit that is closest to the planet/Sun? (Answer: Periapsis.)
- Two rockets have the same thrust force. Rocket A is half the mass of Rocket B. If the thrust force is greater than the sum of each rocket’s mass and drag force, which rocket will accelerate faster? How much faster will this rocket accelerate? (Answer: Rocket A will accelerate twice as fast as Rocket B according to Fnet = ma).
Lesson Extension Activities
References
National Aeronautics and Space Administration, Mars Exploration Program
National Aeronautics and Space Administration, Space Place How Orbits Work
Wertz, James R. and Larson, Wiley J. Space Mission Analysis and Design, 3rd Edition, Space Technology Library, Volume 8, New York, NY: Springer Publishing Company, 1999.
Contributors
Geoffrey Hill, Daria Kotys-Schwartz, Chris Yakacki, Janet Yowell, Malinda Schaefer Zarske © 2004 by Regents of the University of Colorado.
Supporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado Boulder
Acknowledgements
Last modified: September 11, 2015
Filed under: Class Activities, Grades 6-8, Grades 6-8, Lesson Plans
Tags: Aerospace, astronauts, calculations, Class Activities, forces, Grades 6-8, Grades 9-12, Humans in Space, Lesson Plans, Mars, motions, NASA, Physics, trajectory









